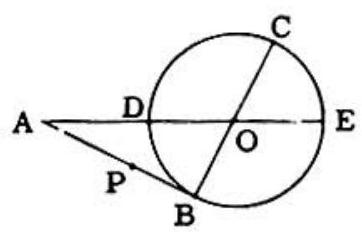
Problem: In this figure the center of the circle is O. AB⊥BC, ADOE is a straight line, AP=AD, and AB has a length twice the radius. Then:
Answer Choices:
A. AP2=PBâ‹…AB
B. APâ‹…DO=PBâ‹…AD
C. AB2=ADâ‹…DE
D. ABâ‹…AD=OBâ‹…AO
E. none of these
Solution:
Since ABAD​=AEAB​,AB2=AD⋅AE
But AE=AD+2r=AD+AB∴AB2=AD(AD+AB)
=AD2+ADâ‹…AB
∴AD2=AB2−AD⋅AB=AB(AB−AD)
Since AP=AD,AP2=AB(AB−AP)=AB⋅PB
