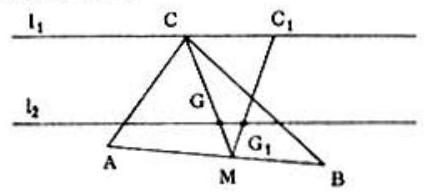
Problem: Given triangle with base fixed in length and position. As the vertex moves on a straight line, the intersection point of the three medians moves on:
Answer Choices:
A. a circle
B. a parabola
C. an ellipse
D. a straight line
E. a curve here not listed
Solution:
Let the vertex move along the straight line to position . Let G be the location of the centroid (the intersection point of the three medians) of ; let be the location of the centroid of .
Since and the line is parallel to line . (If a line divides two sides of a triangle proportionally, it is parallel to the third side.) Therefore, as moves along moves along which is parallel to .