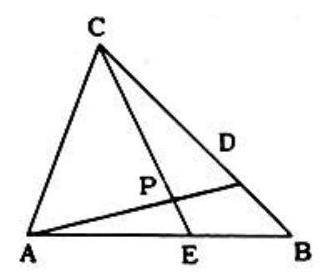
Problem: In triangle ABC lines CE and AD are drawn so that DBCD=13 and EBAE=23. Let r=PECP where P is the intersection point of CE and AD. Then r equals:
Answer Choices:
A. 3
B. 23
C. 4
D. 5
E. 23
Solution:
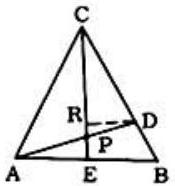
Draw \mathrm{DR} \| \mathrm{AB} \cdot \dfrac{\overline{\mathrm{CR}}}{\overline{\mathrm{RE}}}=\dfrac{\overline{\mathrm{CD}}}{\overline{\mathrm{DB}}}=\dfrac{3}{1}, \dfrac{\overline{\mathrm{RD}}}{\overline{\mathrm{EB}}}=\dfrac{\overline{\mathrm{CD}}}{\overline{\mathrm{CB}}}=\dfrac{3}
∴CR=3RE=3RP+3PE and RD=43 EB
∴CP=CR+RP=4RP+3PE.
Since △RDP∼△EAP,PERP=AERD
∴RD=PERP×AE. But AE=23 EB,∴RD=PERP⋅23 EB
∴43 EB=23 EB⋅PERP,RP=21PE,CP=4⋅21PE+3PE=5PE∴PECP=5