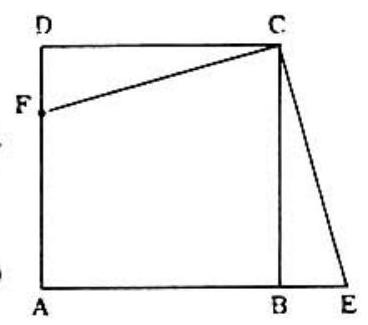
Problem: Point F is taken in side AD of square ABCD. At C a perpendicular is drawn to CF, meeting AB extended at E. The area of ABCD is 256 square inches and the area of triangle CEF is 200 square inches. Then the number of inches in BE is:
Answer Choices:
A. 12
B. 14
C. 15
D. 16
E. 20
Solution:
△CDF≈△CBE(CD=CB, angle DCF= angle BCE),∴CF=CE.
Area (△CEF)=21CE⋅CF=21CE2=200.∴CE2=400.
Area (square) =CB2=256. Since BE2=CE2−CB2=400−256=144,CE=12.