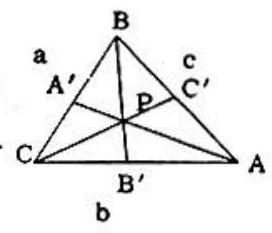
Problem: The magnitudes of the sides of triangle ABC are a,b, and c, as shown, with c≦b≦a. Through interior point P and the vertices A,B,C lines are drawn meeting the opposite sides in A′,B′,C′, respectively. Let s=AA′+BB′+CC′. Then, for all positions of point P,s is less than:
Answer Choices:
A. 2a+b
B. 2a+c
C. 2b+c
D. a+2b
E. a+b+c
Solution:
The length of each of the lines through P must be less than the length of the larger of the two sides of the triangle adjacent to the line through P. To see this let BB' be fixed and allow point P to take a position very close to B′. Then A′ takes a position very close to C so that AA′ is very nearly equal to b, but less than b. Similarly, CC ' remains smaller than a and BB′ remains smaller than a for all interior positions of P}.
∴AA′+BB′+CC′<b+a+a∴s<2a+b.