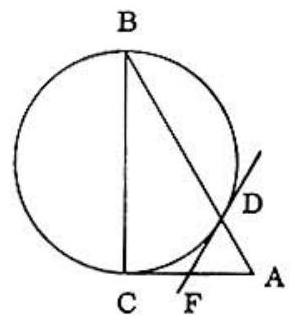
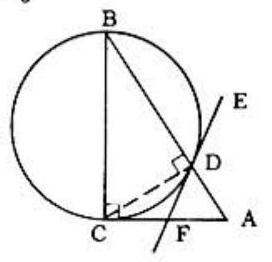
Problem: Let BC of right triangle ABC be the diameter of a circle intersecting hypotenuse AB in D. At D a tangent is drawn cutting leg CA in F. This information is not sufficient to prove that:
Answer Choices:
A. DF bisects CA
B. DF bisects ∠CDA
C. DF=FA
D. ∠A=∠BCD
E. ∠CFD=2∠ A
Solution:
∠A=∠BCD (Why?), DF=CF (Why?) ∴∠DCF=∠CDF
∠BCD=90∘−∠DCF,∠FDA=90∘−∠CDF
∴∠FDA=∠BCD=∠A∴DF=FA=CF, that is, DF bisects CA. Also ∠CFD=∠FDA+∠A=2∠ A.
The given information is, therefore, sufficient to prove choices (A),(C),(D), and (E). Eor choice (B) to be true, segments CD and AD would have to be equal, but such equality can not hold for all possible positions of point D.