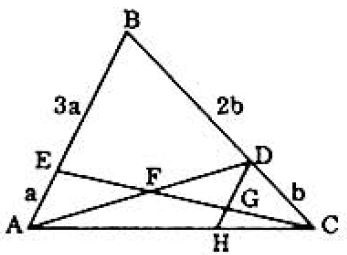
Problem: Point E is selected on side AB of triangle ABC in such a way that AE:EB=1:3 and point D is selected on side BC so that CD:DB=1:2. The point of intersection of AD and CE is F. Then FCEF+FDAF is:
Answer Choices:
A. 54
B. 45
C. 23
D. 2
E. 25
Solution:
Draw DGH ∥AB∴DG:3a=b:3 b;DG=a=EA
∴EF=FG and AF=FD so that AF/FD=1
Also DH:4a=b:3 b,DH=4a/3 and GH=DH−DG=a/3
∴GC=31EC and EG=32EC, and, since EF=FG,FC=32EC
\therefore E F / F C=\dfrac{1}{2} \quad \therefore \overline{E F} / \overline{F C}+\overline{\mathrm{AF}} / \overline{\mathrm{FD}}=\dfrac{1}{2}+1=\dfrac{3}
.jpg)