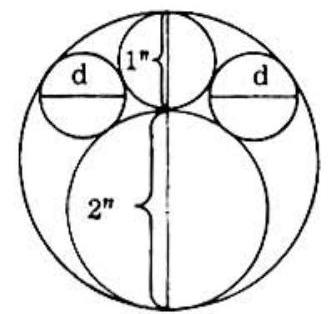
Problem: A foreman noticed an inspector checking a 3 ′ ′ 3 ′ ′ 2 ′ ′ 2 ′ ′ 1 ′ ′ 1 ′ ′ d d
Answer Choices:
A. 0.87 0 . 8 7
B. 0.86 0 . 8 6
C. 0.83 0 . 8 3
D. 0.75 0 . 7 5
E. 0.71 0 . 7 1 Solution:
O A ‾ = 1 2 + r , O ′ A ‾ = 1 + r , B A ‾ = 1 1 2 − r O A = 2 1 + r , O ′ A = 1 + r , B A = 1 2 1 − r
Area ( △ O B A ) = 2 ( △ O B A ) = 2 ( △ B O ′ A ) ( △ B O ′ A )
Semiperimeter (\triangle \mathrm{OBA})=\dfrac{1}{2}\left(\dfrac{1}{2}+r+1+\dfrac{3}{2}-r\right)=\dfrac{3}
Semiperimeter \left(\triangle B^{\prime} O A\right)=\dfrac{1}{2}\left(\dfrac{3}{2}-r+\dfrac{1}{2}+1+r\right)=\dfrac{3}
∴ 3 2 ( 1 − r ) ( 1 2 ) r = 2 3 2 ( r ) ( 1 ) ( 1 2 − r ) ∴ 7 r = 3 , r = 3 7 , d = 8 7 ≈ . 86 ∴ 2 3 ( 1 − r ) ( 2 1 ) r = 2 2 3 ( r ) ( 1 ) ( 2 1 − r ) ∴ 7 r = 3 , r = 7 3 , d = 7 8 ≈ . 8 6
or
Draw the altitude h h A A
\left(\dfrac{1}{2}+r\right)^{2}-t^{2}=\left(\dfrac{1}{2}-r\right)^{2}-(1-t)^{2}, t=2 r-\dfrac{1}{2}, h^{2}=3 r-3 r^
Since Area ( Δ O A O ′ ) = 1 2 h ⋅ 3 2 = ( 3 2 + r ) ( r ) ( 1 ) ( 1 2 ) ( Δ O A O ′ ) = 2 1 h ⋅ 2 3 = ( 2 3 + r ) ( r ) ( 1 ) ( 2 1 ) 9 16 h 2 = 9 16 ( 3 r − 3 r 2 ) = 3 4 r + 1 2 r 2 ∴ r = 3 7 1 6 9 h 2 = 1 6 9 ( 3 r − 3 r 2 ) = 4 3 r + 2 1 r 2 ∴ r = 7 3
.jpg)
.jpg)