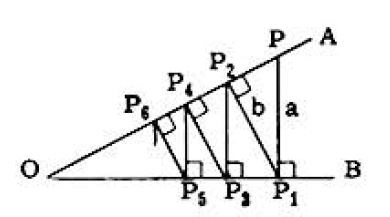
Problem: Given distinct straight lines OA and OB. From a point in OA a perpendicular is drawn to OB; from the foot of this perpendicular a line is drawn perpendicular to OA. From the foot of this second perpendicular a line is drawn perpendicular to OB; and so on indefinitely. The lengths of the first and second perpendiculars are a and b, respectively. Then the sum of the lengths of the perpendiculars approaches a limit as the number of perpendiculars grows beyond all bounds. This limit is:
Answer Choices:
A. a−bb
B. a−ba
C. a−bab
D. a−bb2
E. a−ba2
Solution:
ΔP3P2P1∼ΔP2P1P∴P3P2:b=b:a,P3P2=b2/a
ΔP4P3P2∼ΔP3P2P1∴Pˉ4P3:b2/a=b2/a:b,P4P3=b2/a2
Similarly P5P4=b4/a3 and so forth. The limiting sum is a+b+ab2+a2b4+a3b4+…
=a+1−b/ab=a+a−bab=a−ba2