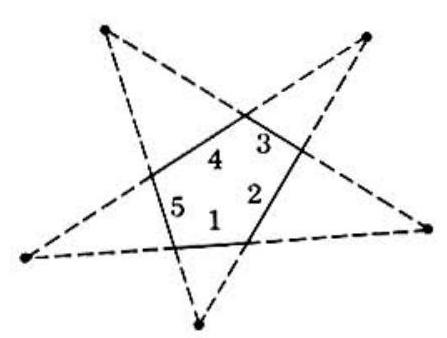
Problem: An 'n-pointed star' is formed as follows: the sides of a convex polygon are numbered consecutively 1,2,⋯,k,⋯,n,n≧5; for all n values of k, sides k and k+2 are non-parallel, sides n+1 and n+2 being respectively identical with sides 1 and 2; prolong the n pairs of sides numbered k and k+2 until they meet.
(A figure is shown for the case n=5 ).
Let S be the degree-sum of the interior angles at the n points of the star; then S equals:
Answer Choices:
A. 180
B. 360
C. 180(n+2)
D. 180(n−2)
E. 180(n−4)
Solution:
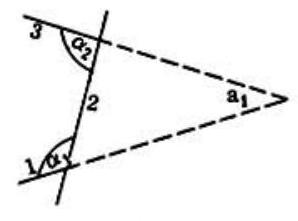
Let the measures of the angles at the n points be a1,a2,…,an and let α1,α2,…,αn be the measures of the interior angles of the polygon, with αn=α1. We have a1=180−(180−α1)−(180−α2)=α1+α2−180, a2=α2+α3−180,…,an=αn−1+αn−180. Summing, we have a1+a2+…+an=2(α1+α2+…+αn)−n⋅180
∴S=2((n−2)180)−n⋅180=180(n−4)