Problem: Given a set consisting of two undefined elements "pib" and "maa", and the four postulates: : Every pib is a collection of maas, : Any two distinct pibs have one and only one maa in common, : Every maa belongs to two and only two pibs, : There are exactly four pibs.
Consider the three theorems: : There are exactly six maas, : There are exactly three maas in each pib, : For each maa there is exactly one other maa not in the same pib with it. The theorems which are deducible from the postulates are:
Answer Choices:
A. only
B. and only
C. and only
D. and only
E.
Solution:
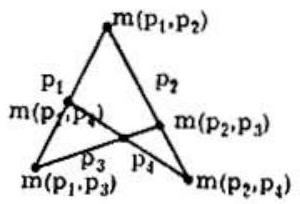
One method of establishing theorems for a finite geometry is to construct a model. In the one shown here the maa, , for example, is common to and . The maa common to and should be labeled . In this model each of the four postulates is satisfied. Since there must be a maa for every pair of pibs, there must be a maa for each of the pairs ( , and , six in all. This establishes . Each pib consists of exactly three maas. For example, consists of , , and . This establishes . For there is not in or , and, similarly, for each of the other maas. This establishes .
or
By and there is a one - one correspondence between the set of maas and the set of pairs of pibs. The four pibs yield six pairs (listed above) and so is true. Each pib belongs to three of the six pairs and so is true. Each pair of pibs is disjoint from one other pair (for example, the pair is disjoint from the pair ) and so is true.