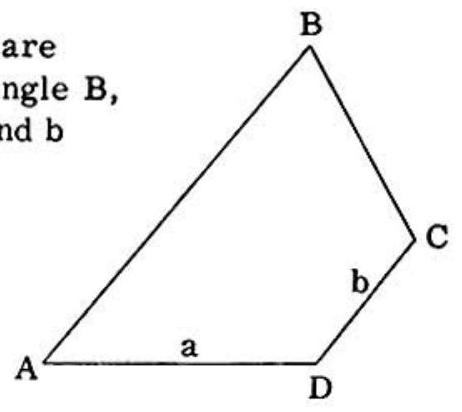
Problem: In the accompanying figure, segments and are parallel, the measure of angle is twice that of angle , and the measures of segments and are and respectively. Then the measure of is equal to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the bisector of angle be drawn and intersect at . Then is a parallelogram and an isosceles triangle. The measures of , and hence .