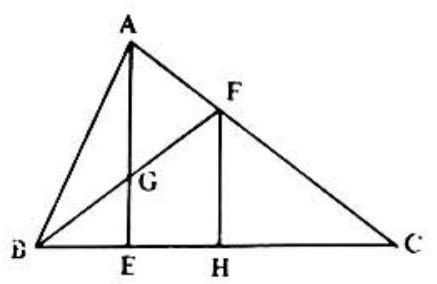
Problem: In triangle ABC, point F divides side AC in the ratio 1:2. Let E be the point of intersection of side BC and AG where G is the midpoint of BF. Then point E divides side BC in the ratio
Answer Choices:
A. 1:4
B. 1:3
C. 2:5
D. 4:11
E. 3:8
Solution:
Draw $\mathrm{FH} parallel to $\mathrm{AE} . Then BE=EH because BG=GF. Also 2EH=HC because 2AF=FC.∴3BE=EH+HC=EC.∴E divides BC in the ratio 1:3.
.jpg)