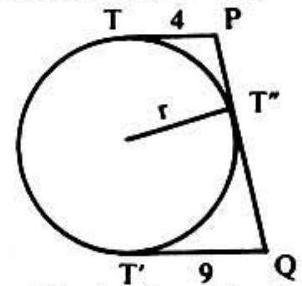
Problem: In the adjoining figure TP and T′Q are parallel tangents to a circle of radius r, with T and T′ the points of tangency. PT′′Q is a third tangent with T′′ as point of tangency. If TP=4 and T′Q=9 then r is
Answer Choices:
A. 25/6
B. 6
C. 25/4
D. a number other than 25/6,6,25/4
E. not determinable from the given information
Solution:
Since TP=T′P,OT=OT′=r, and ∠PT′O=. PTO=90∘, we have △OTP≈△OT′P. Similarly △OT′Q≈△OT′Q. Letting x=∠TOP=∠POT′. and y=T′QQ=−QOT′ we obtain 2x+2y−180∘ But this implies that ∠POQ=x+y=90∘. Therefore △POQ is a right triangle with altitude OT. Since the altitude drawn to the nypotenuse of a right triangle is the mean proportion of the segments it cuts, we have r4−9r or r=6.