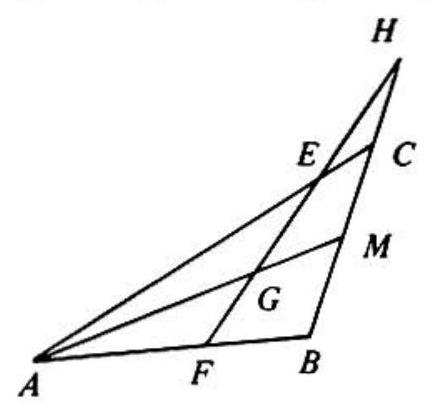
Problem: In triangle ABC shown in the adjoining figure, M is the midpoint of side BC, AB=12 and AC=16. Points E and F are taken on AC and AB, respectively, and lines EF and AM intersect at G. If AE=2AF then EG/GF equals
Answer Choices:
A. 3/2
B. 4/3
C. 5/4
D. 6/5
E. not enough information given to solve the problem
Solution:
Construct line CP parallel to EF and intersecting AB at P. By proportionality AP =8. Let a,x,y,α,β,δ and θ be as shown in the adjoining diagram. Then
sinαa=sinθ12;sinβa=sin(180∘−θ)16;sinαsinβ=43.
Therefore,
sinαx=sinδ8;sinβy=sin(180∘−δ)16;
and
GFEG=xy=2sinαsinβ=23.
OR
In the adjoining figure side BC extended through C intersects EF extended through E at H. Applying Menelaus' theorem to △FBH and △HCE with AM as the transversal, we obtain
GFGHABAFMHMB=1,GEGHACAEMHMC=1,
respectively. Since MC=MB and AE=2AF, dividing the first equation by the second yields
GFGE=2ACAB=2⋅1612=23.
Menelaus' theorem: The six segments determined by a transversal on the sides of a triangle are such that the product of three non-consecutive segments is equal to the product of the remaining three.
.jpg)
.jpg)