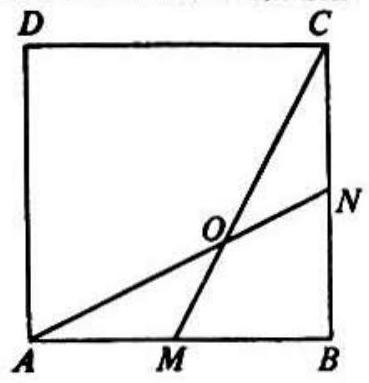
Problem: In the adjoining figure and are adjacent sides of square is the midpoint of is the midpoint of ; and and intersect at . The ratio of the area of to the area of is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
In the adjoining figure diagonals and are drawn. Since is a square and bisect each other at at right angles. If denotes the length of a side of the square, then . Now is the intersection of the medians of triangle , so that . Thus the area of is . The area of is then , and the required ratio is .
.jpg)
OR
Introduce coordinates with respect to which is the unit inverval on the positive -axis and is the unit interval on the positive -axis, and find the coordinates of by solving simultaneously the equations for the lines and . Calculate the area of by drawing perpendiculars from to and .