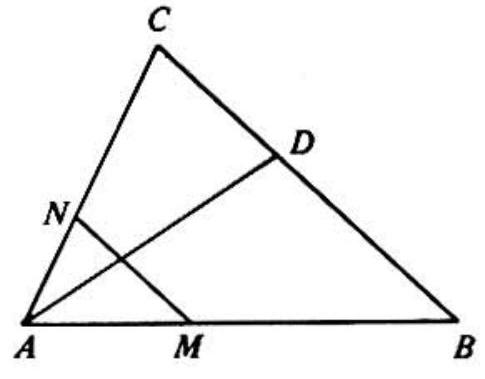
Problem: In acute triangle ABC the bisector of ∠A meets side BC at D. The circle with center B and radius BD intersects side AB at M; and the circle with center C and radius CD intersects side AC at N. Then it is always true that
Answer Choices:
A. ∠CND+∠BMD−∠DAC=120∘
B. AMDN is a trapezoid
C. BC is parallel to MN
D. AM−AN=23(DB−DC)​
E. AB−AC=23(DB−DC)​
Solution:
In the adjoining figure CDBD​=ACAB​, since the bisector of an angle of a triangle divides the opposite side into segments which are proportional to the two adjacent sides. Since CN=CD and BM=BD, we have CNBM​=ACAB​, which implies MN is parallel to CB. Statements (A), (B), (D) and (E) are false if
∠A=90∘−θ,∠B=60∘ and ∠C =30∘+θ, where θ is any sufficiently small positive angle.
