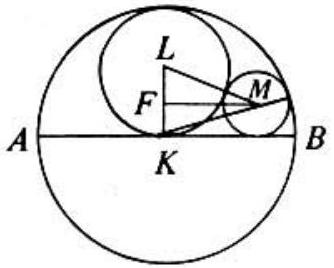
Problem: In the adjoining figure, circle has diameter ; circle is tangent to circle and to at the center of circle ; and circle is tangent to circle , to circle and to . The ratio of the area of circle to the area of circle is
.jpg)
Answer Choices:
A.
B.
C.
D.
E. Not an integer
Solution:
In the adjoining figure, is parallel to and intersects at . Let , and be the radii of the circles with centers and , respectively. Applying the Pythagorean theorem to and yields
Equating the right members of these equalities yields .
Therefore the desired ratio is 16 .