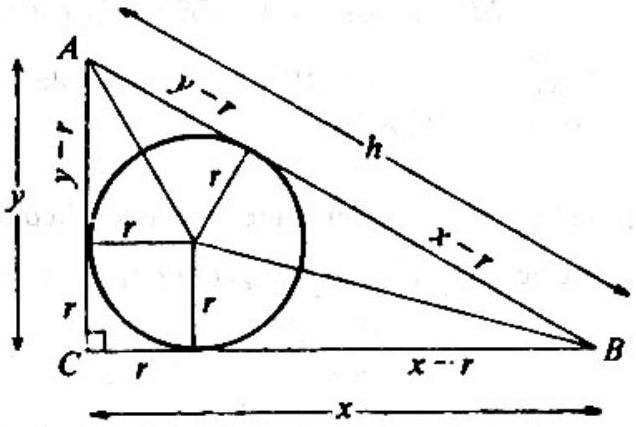
Problem: The length of the hypotenuse of a right triangle is h, and the radius of the inscribed circle is r. The ratio of the area of the circle to the area of the triangle is
Answer Choices:
A. h+2rπr
B. h+rπr
C. 2h+rπr
D. h2+r2πr2
E. none of these
Solution:
In the adjoining figure, x and y are the lengths of the legs of the triangle, so that h=(y−r)+(x−r)
=x+y−2r,
x+y=h+2r;
x2+y2=h2.
The area of the triangle ABC is
21xy=21[2(x+y)2−(x2+y2)]=41[(h+2r)2−h2]=hr+r2
Thus the desired ratio is hr+r2πr2=h+rπr.