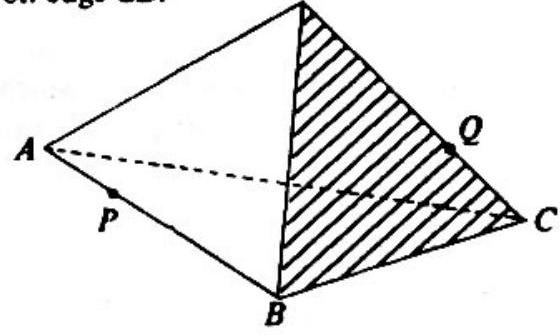
Problem: The edges of a regular tetrahedron with vertices and each have length one. Find the least possible distance between a pair of points and . where is on edge and is on edge .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Since the shortest path between a point and a line is the line segment drawn perpendicularly from the poine to the line, the desired minimum distance is obtained by symmetry by choosing and to .ie the midpoints of and , respectively.
Since and are altitudes of equilateral triangles and . respectively, . Since is the midpoint of side .
Applying the Pythagorean theorem to yields