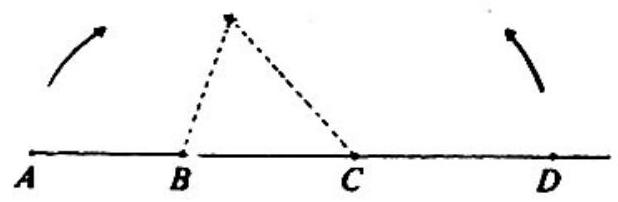
Problem: Points A,B,C and D are distinct and lie, in the given order, on a straight line. Line segments AB,AC and AD have lengths x,y and z, respectively. If line segments AB and CD may be rotated about points B and C, respectively, so that points A and D coincide, to form a triangle with positive area, then which of the following three inequalities must be satisfied?
I x<2z II y<x+2z III y<2z
Answer Choices:
A. I only
B. II only
C. I and II only
D. II and III only
E. I, II and III
Solution:
Since the length of any side of a triangle is less than the sum of the lengths of the other sides,
x<y−x+z−y=z−x, which implies x<2zy−x<x+z−y, which implies y<x+2zz−y<x+y−x, which implies y>2z.
Therefore, only statements I and II are true.