Problem:
Let and be three parallel chords of a circle on the same side of the center. The distance between and is the same as the distance between and . The lengths of the chords are and . The radius of the circle is
Answer Choices:
A.
B.
C.
D.
E. not uniquely determined by the given information
Solution:
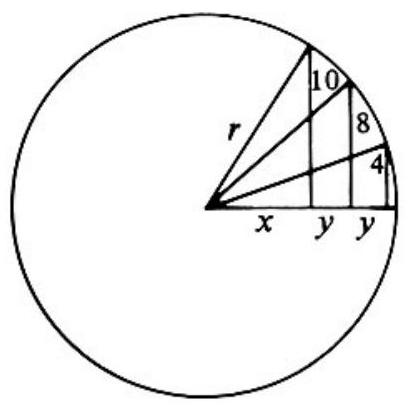
The adjoining figure is constructed from the given data. We let be the radius, the distance from the center of the circle to the closest chord, and the common distance between the chords. The Pythagorean theorem provides three equations in , and :
Subtracting the first equation from the second yields , and subtracting the second equation from the third yields . Equating the right sides of these last two equations and collecting like terms yields . Thus, ; and by repeated subThus, ; and by repeated substitutions into the equations above, .