Problem:
Four balls of radius are mutually tangent, three resting on the floor and the fourth resting on the others. A tetrahedron, each of whose edges has length , is circumscribed around the balls. Then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
.jpg)
A smaller regular tetrahedron circumscribing just one of the balls may be formed by introducing a plane parallel to the horizontal face as shown in Figure . Let the edge of this tetrahedron be . Next construct the quadrilateral , where and are centers of two of the balls. By the symmetry of the ball tetrahedron configuration the sides
are parallel and equal. It follows that .
Thus, , and our problem reduces to that of determining .
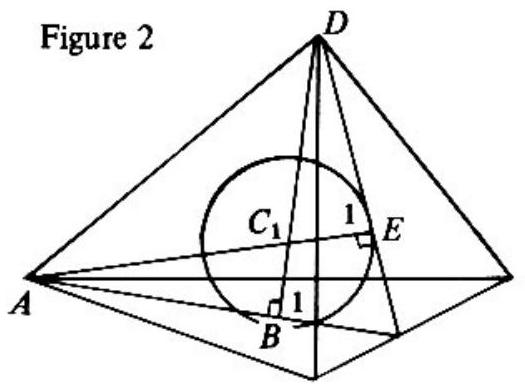
In , in Figure , has a length of one radius less than the length of altitudes and of the smaller tetrahedron; and has length , since is the center of a face. Applying the Pythagorean theorem to , yields
and applying the Pythagorean theorem to yields
Solving the second equation for , substituting this value for in the first equation, and solving the resulting equation for the positive value of yields