Problem:
In triangle ABC,∠CBA=72∘,E is the middpoint of side AC, and D is a point on side BC such that 2BD=DC;AD and BE intersect at F. The ratio of the area of △BDF to the area of quadrilateral FDCE is
Answer Choices:
A. 51
B. 41
C. 31
D. 52
E. none of these
Solution:
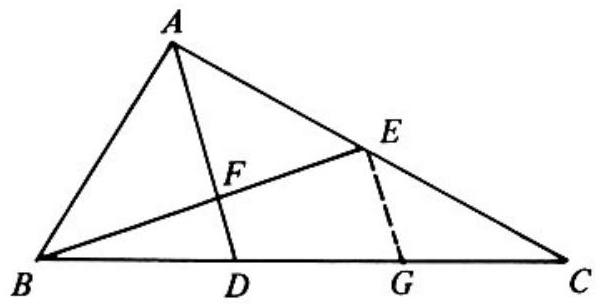
In the adjoining figure the line segment from E to G, the midpoint of DC, is drawn. Then
area △EBG=(32)( area △EBC) area △BDF=(41)( area △EBG)=(61)( area △EBC)
(Note that since EG connects the midpoints of sides AC and DC in △ACD, EG is parallel to AD). Therefore, area FDCE=(65)( area △EBC) and
( area FDCE)( area △BDF)=51
The measure of ∠CBA was not needed.