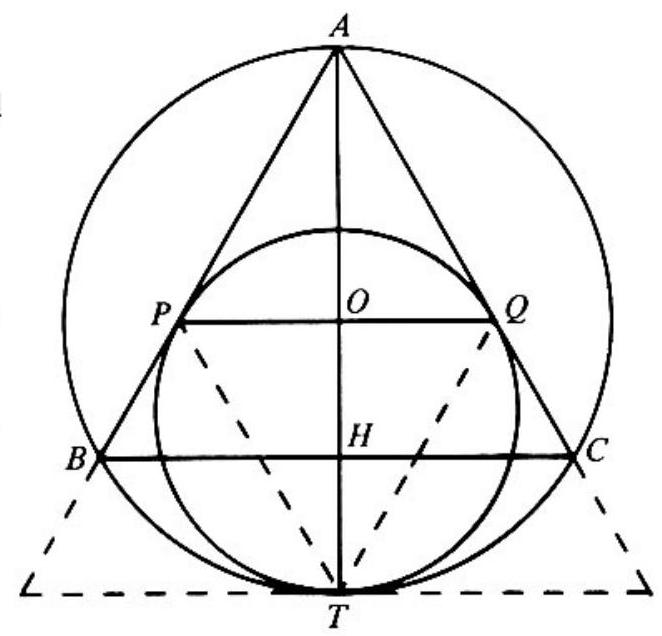
Problem:
Equilateral is inscribed in a circle. A second circle is tangent internally to the circumcircle at and tangent to sides and at points and . If side has length , then segment has length
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let and be the points at which and , respectively, intersect diameter . Sides and form a portion of the equilateral triangle circumscribing the smaller circle and tangent to the smaller circle at . Therefore, is an equilateral triangle. Since is an equilateral triangle with a side in common with . Thus and is the center of the larger circle. This implies , so that .