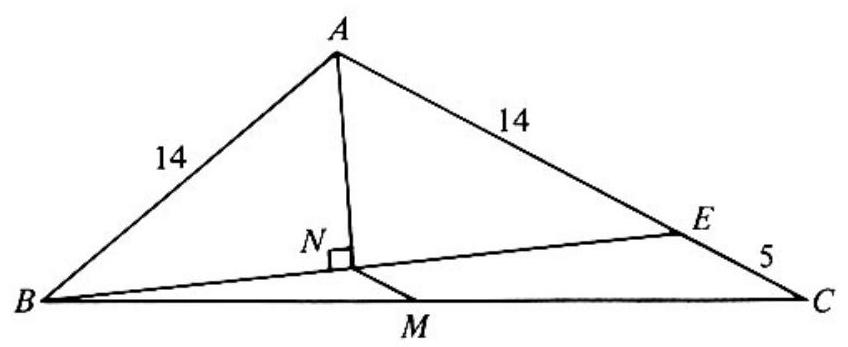
Problem:
In △ABC,M is the midpoint of side BC,AN bisects ∠BAC,BN⊥AN and θ is the measure of ∠BAC. If sides AB and AC have lengths 14 and 19, respectively, then length MN equals
Answer Choices:
A. 2
B. 25
C. 25−sinθ
D. 25−21sinθ
E. 25−21sin(21θ)
Solution:
In the adjoining figure, BN is extended past N and meets AC at E. Triangle BNA is congruent to △ENA, since ∠BAN=∠EAN,AN=AN and ∠ANB=∠ANE.
Therefore N is the midpoint of BE and AB=AE=14. Thus EC=5. Since M is given to be the midpoint of BC,MN joins the midpoints of two sides of △BEC and MN =21(EC)=25.
.jpg)