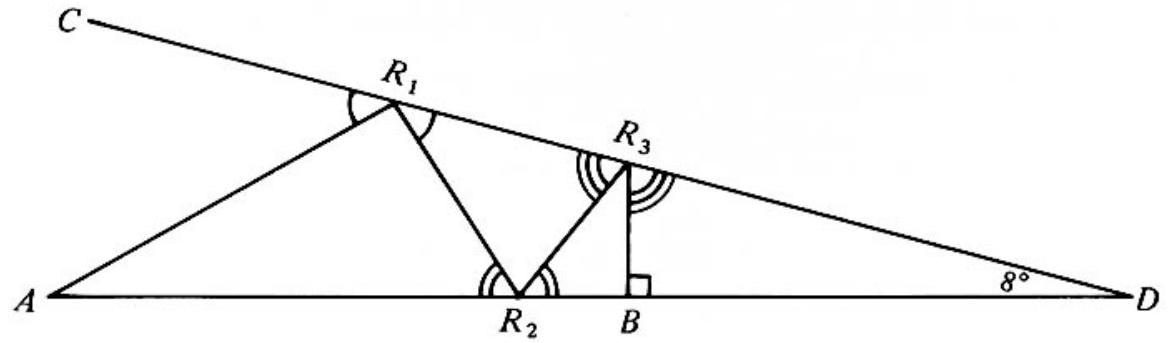
Problem:
A ray of light originates from point A and travels in a plane, being reflected n times between lines AD and CD, before striking a point B (which may be on AD or CD) perpendicularly and retracing its path to A. If ∠CDA=8∘, what is the largest value n can have?
Answer Choices:
A. 6
B. 10
C. 38
D. 98
E. There is no largest value.
Solution:
Let ∠DAR1=θ and let θi be the (acute) angle the light beam and the reflecting line form at the ith point of reflection. Applying the theorem on exterior angles of triangles to △AR1D, then successively to the triangles ΔRi−1RiD,2⩽i⩽n, and finally to △RnBD yields
θ1=θ+8∘θ2=θ1+8∘=θ+16∘θ3=θ2+8∘=θ+24∘−−−−−−−−−−−θn=θn−1+8∘=θ+(8n)∘90∘=θn+8∘=θ+(8n+8)∘.
But θ must be positive. Therefore,
0⩽θn=90−(8n+8)⩽882<11
If θ=2∘, then n takes its maximum value of 10.