Problem:
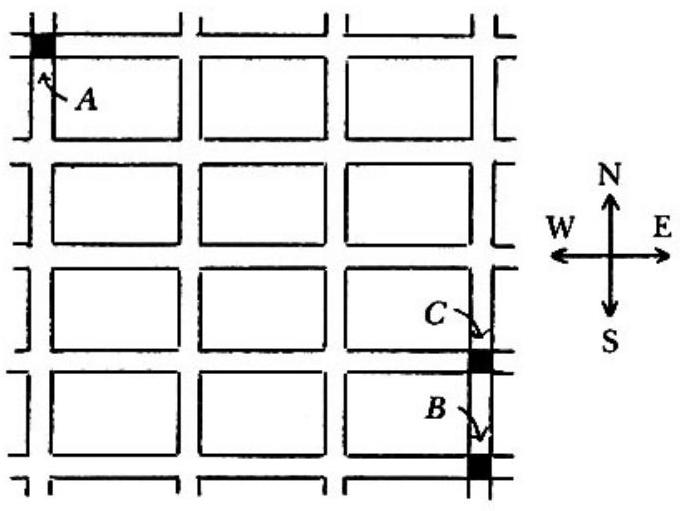
The adjoining figure is a map of part of a city: the small rectangles are blocks and the spaces in between are streets. Each morning a student walks from intersection to intersection , always walking along streets shown, always going east or south. For variety, at each intersection where he has a choice, he chooses with probability (independent of all other choices) whether to go east or south. Find the probability that, on any given morning, he walks through intersection .
Answer Choices:
A.
B.
C.
D.
E.
Solution:
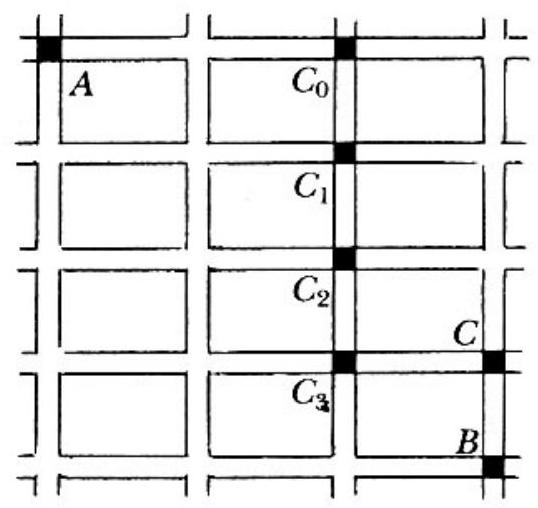
The probability that the student passes through is the sum from to of the probabilities that he enters intersection in the adjoining figure and goes east. The number of paths from to is , because each such path has eastward block segments and they can occur in any order. The probability of taking any one of these paths to and then going east is because there are intersections along the way (including and ) where an independent choice with probability is made. So the answer is
Alternate Solution.
Less elegantly, one may construct a tree-diagram of the respective probabilities, obtaining the values step-by-step as shown in the scheme to the right (the final also serves as a check on the computations).
It is important to recognize that not all twenty of the thirty five paths leading from to through are equally likely; hence answer is incorrect!
.jpg)