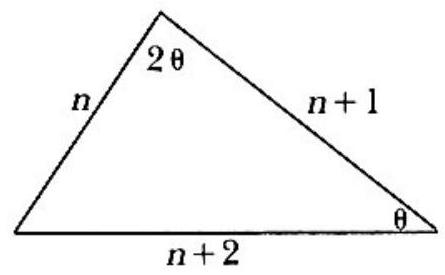
Problem:
The lengths of the sides of a triangle are consecutive integers, and the largest angle is twice the smallest angle. The cosine of the smallest angle is
Answer Choices:
A. 43
B. 107
C. 32
D. 149
E. none of these
Solution:
In the adjoining figure, n denotes the length of the shortest side, and θ denotes the measure of the smallest angle. Using the law of sines and writing 2sinθcosθ for sin2θ yields
nsinθ=n+22sinθcosθ,cosθ=2nn+2.
Equating 2nn+2 to the expression of cosθ obtained from the law of cosines yields
2nn+2=2(n+1)(n+2)(n+1)2+(n+2)2−n2=2(n+1)(n+2)(n+1)(n+5)=2(n+2)n+5
Thus n=4 and cosθ=4(2)4+2=43.