Problem:
Let f(x)=∣x−2∣+∣x−4∣−∣2x−6∣, for 2⩽x⩽8. The sum of the largest and smallest values of f(x) is
Answer Choices:
A. 1
B. 2
C. 4
D. 6
E. none of these
Solution:
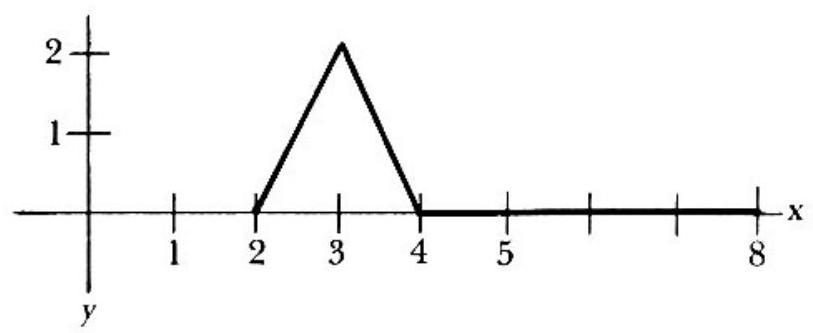
When 2⩽x⩽3,f(x)=(x−2)−(x−4)+(2x−6)=−4+2x. Similar algebra shows that when 3⩽x⩽4,f(x)=8−2x; and when 4⩽x⩽8,f(x)=0. The graph of f(x) given in the adjoining figure shows that the maximum and minimum of f(x) are 2 and 0, respectively.