Problem:
Triangle has a right angle at . If , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
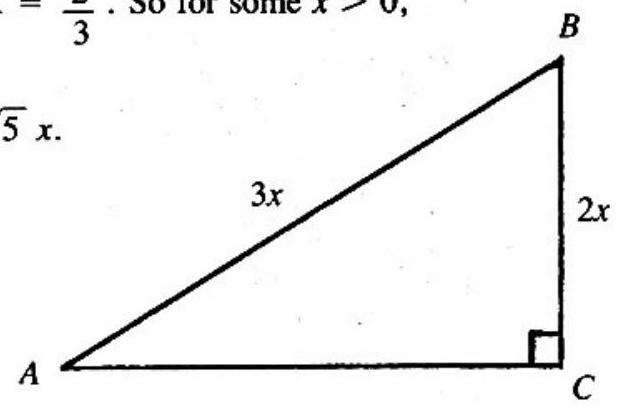
In the figure, . So for some , and .
Thus .
Problem:
Triangle has a right angle at . If , then is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
In the figure, . So for some , and .
Thus .
