Problem:
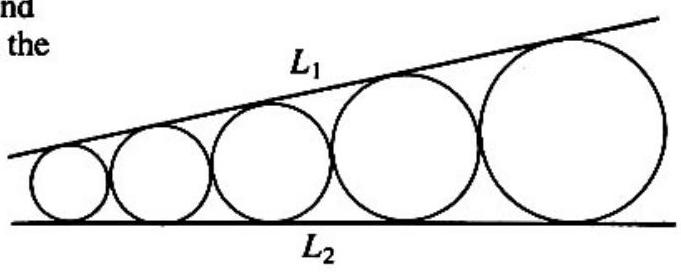
In the adjoining figure the five circles are tangent to one another consecutively and to the lines and . If the radius of the largest circle is and that of the smallest one is , then the radius of the middle circle is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
We claim that the ratio of consecutive radii is constant, that is, the sequence of radii form a geometric progression. It follows that this ratio is and that the middle radius is .
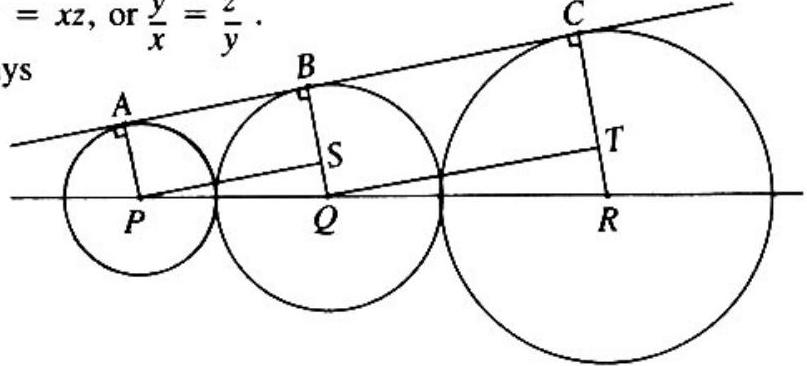
The claim should be intuitive-the picture for any two consecutive circles looks the same except for a change of scale-but here is a proof. In the figure below, three consecutive circles are shown. Their centers and are collinear, on the line bisecting the angle formed by the two tangents. Let and be the points of tangency, and let be segments parallel to the upper tangent as shown. Then . If we let be the radii from smallest to largest, then .
Thus becomes , which simplifies to , or . This last equation says that the ratio of consecutive radii is constant, as claimed.