Problem:
A point lies in the same plane as a given square of side . Let the vertices of the square, taken counterclockwise, be and . Also, let the distances from to and , respectively, be and . What is the greatest distance that can be from if
Answer Choices:
A.
B.
C.
D.
E.
Solution:
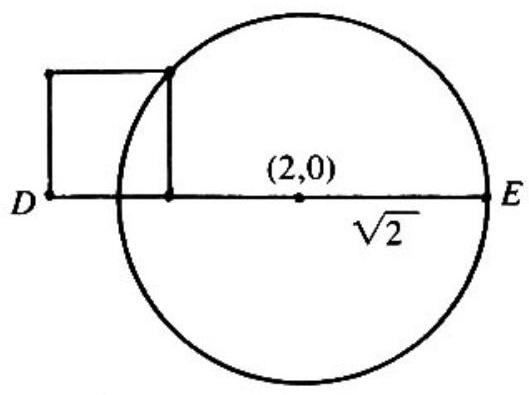
Let the square be placed in the coordinate plane as in the first figure: is placed at the origin so that algebraic expressions for the distance from it will be easy to interpret. Then becomes
.jpg)
which simplifies to , that is, . Thus the locus of is a circle with center and radius . From the second figure it is clear that the farthest point on this circle from is .