Problem:
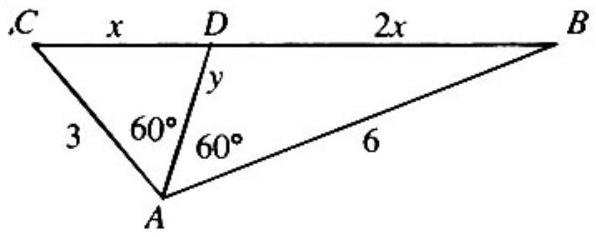
Point D is on side CB of triangle ABC. If ∠CAD=∠DAB=60∘,AC=3 and AB=6, then the length of AD is
Answer Choices:
A. 2
B. 2.5
C. 3
D. 3.5
E. 4
Solution:
Let AD=y. Since AD bisects ∠BAC, we have CDDB=ACAB=2; so we may set CD=x,DB=2x as in the figure. Applying the Law of Cosines to △CAD and △DAB, we have
x2=32+y2−3y(2x)2=62+y2−6y.
Subtracting 4 times the first equation from the second yields 0=−3y2+6y=−3y(y−2). Since y=0,y=2.
Alternate solution. Extend CA to E so that BE∥DA as in the new figure. Then △ABE is equilateral: ∠BEA=∠DAC by corresponding angles, ∠ABE=∠BAD by alternate interior angles, and ∠EAB=180∘−120∘. Since △BEC∼△DAC, we have BEDA=CECA, or 6DA=93.
So DA=2.
.jpg)