Problem:
The diagram to the right shows several numbers in the complex plane. The circle is the unit circle centered at the origin. One of these numbers is the reciprocal of . Which one?
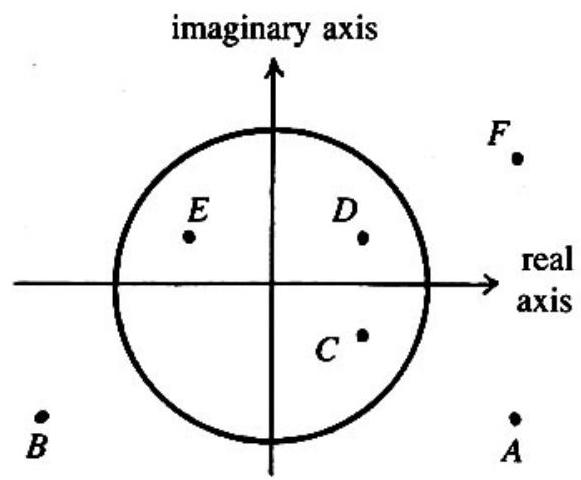
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Write as , where we see from the diagram that and . Since
we see that the reciprocal of is in quadrant IV, since the real part on the right is positive and the imaginary coefficient is negative. Also, the magnitude of the reciprocal is
Thus the only possibility is point .
Alternate solution. For any complex number , the argument (standard reference angle) of is the negative of the argument of , and the modulus (magnitude) of is the reciprocal of the modulus of . (Quick proof: if , then .) Applying this to the point , its reciprocal must be in quadrant IV, inside the unit circle. The only possibility is point .