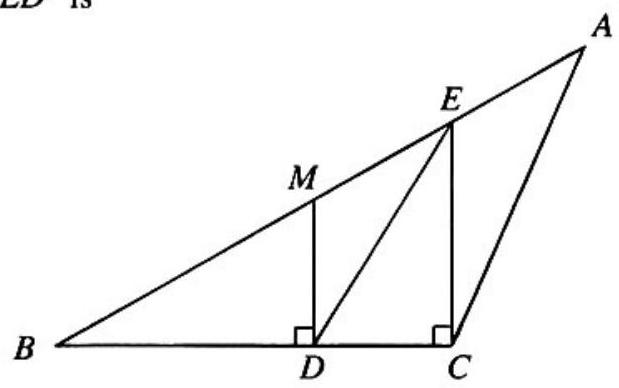
Problem:
In the obtuse triangle ABC,AM=MB,MD⊥BC,EC⊥BC. If the area of △ABC is 24, then the area of △BED is
Answer Choices:
A. 9
B. 12
C. 15
D. 18
E. not uniquely determined
Solution:
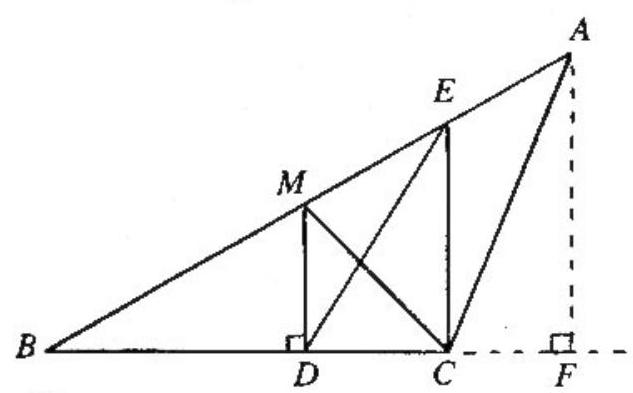
Draw in MC as in the adjoining figure. Then △DMC and △DME have the same area, as they have the same base MD and equal altitudes on that base. Thus
Area △BMC= Area △BED
Moreover, as shown below,
Area △BMC=21 Area △BAC
Thus
Area △BED=21Area △BAC=12.
As for the claim in the second display, since M is the midpoint of BA, altitude MD of △BMC is one half altitude AF of △BAC. Since the triangles have the same base BC, the claim follows.
Alternately, one proves the claim by noting that
Area △BMC=21(BM)(BC)sinB=21[21(BA)(BC)sinB]=21 Area △BAC