Problem:
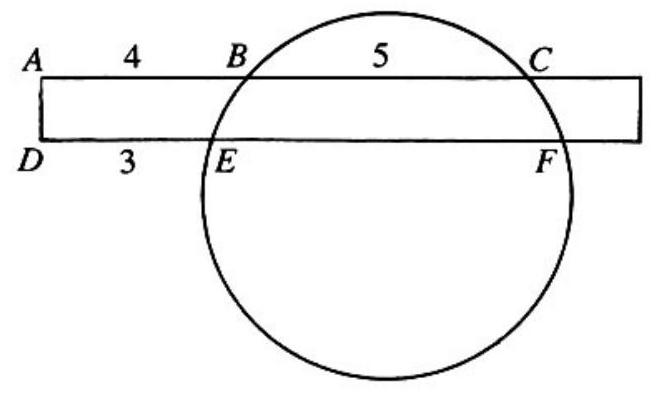
A rectangle intersects a circle as shown: and . Then equals
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Draw in the perpendicular bisector of chord , as shown in the adjoining figure. This bisector must go through the center of the circle. Since is perpendicular to chord as well, it bisects . Since , we have . Thus
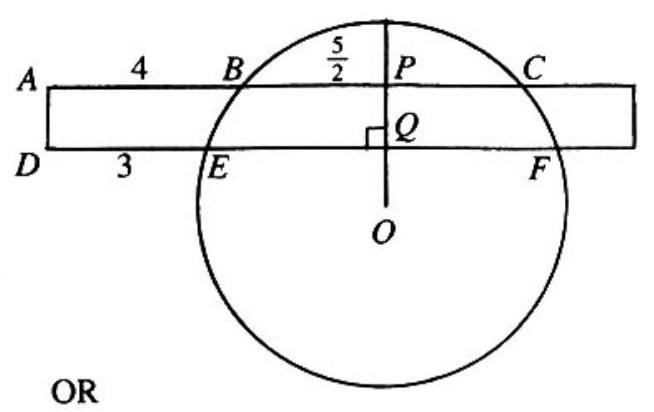
Drop perpendiculars and as shown in the second figure, yielding rectangles and . Then , and by symmetry, . Also, , so
.jpg)