Problem:
The number of distinct solutions of the equation
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The equation is satisfied by precisely those for which the vertical distance between the graph of and the graph of is . These two graphs are sketched in the adjoining figure; the latter graph is -shaped with vertex and sides of slope . Thus there are exactly two values which satisfy the original equation, because the vertical distance between the graphs increases steadily as one moves right or left from , and the vertical distance for that is .
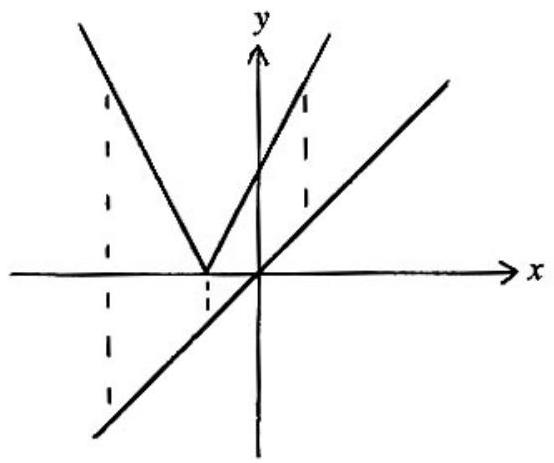
Either or , yielding and , respectively. In the first case one must have , while in the second case, must hold. In the first case, must equal or , yielding and , which are solutions. In the second case, must equal or , and hence and ; however, these values violate the condition and therefore do not satisfy the original equation.