Problem: 8 c m 3 8 c m 3 32 c m 2 3 2 c m 2
Answer Choices:
A. 28 2 8
B. 32 3 2
C. 36 3 6
D. 40 4 0
E. 44 4 4
Solution:
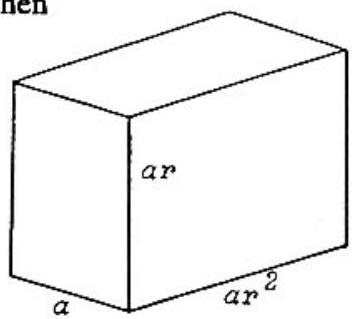
Label the edges of the solid a , a r a , a r a r 2 a r 2
Volume = a ( a r ) ( a r 2 ) = 8 , or a r = 2. Surface Area = 2 a 2 r + 2 a 2 r 2 + 2 a 2 r 3 = 32 = 2 ( a r ) ( a + a r + a r 2 ) = 4 ( a + a r + a r 2 ) . Volume Surface Area = a ( a r ) ( a r 2 ) = 8 , or a r = 2 . = 2 a 2 r + 2 a 2 r 2 + 2 a 2 r 3 = 3 2 = 2 ( a r ) ( a + a r + a r 2 ) = 4 ( a + a r + a r 2 ) .
But this last expression is just the sum of the edge lengths.
Note 1. One can also solve for a a r r 3 − 5 , 2 3 − 5 , 2 3 + 5 3 + 5
Note 2. For any rectangular solid with volume 8 8