Problem:
Consider the graphs of and , where is a positive constant and and are real variables. In how many points do the two graphs intersect?
Answer Choices:
A. exactly
B. exactly
C. at least , but the number varies for different positive values of
D. for at least one positive value of
E. none of these
Solution:
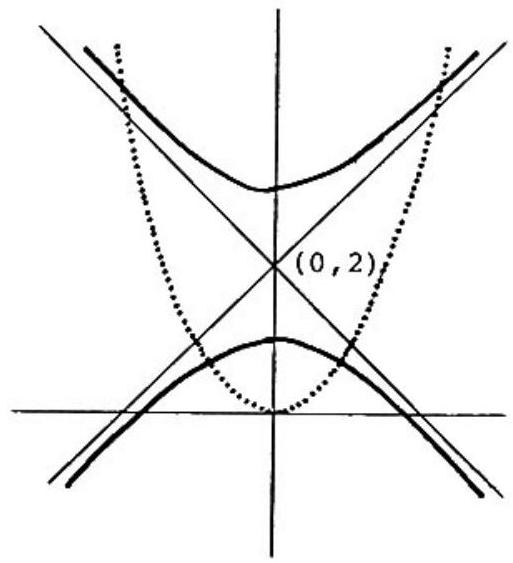
Rearrange the terms and complete the square for the second equation to obtain
whose graph is a hyperbola with center , vertices at and , and asymptotes . The graph of is a parabola opening upward with its vertex at the origin for all positive values of . Therefore there are two distinct points of intersection between the parabola and the lower branch of the hyperbola. The equation of the upper branch of the hyperbola is . For any given positive , if the absolute value of is large enough, then . Since when , the parabola must also intersect the upper branch of the hyperbola in two distinct points for any given positive value of .
We show that the system of equations
has exactly four distinct solutions for any . First, multiply by , eliminate using , and simplify, obtaining
Since all these steps are reversible, the system and has the same solution pairs as the system and . Furthermore, and has two distinct solution pairs () for each positive solution to alone, namely, () and . So it suffices to show that has exactly two solutions, both positive. By the quadratic formula,
Since the discriminant in equation is positive for , there are two real roots. Since the constant term of is positive and the coefficient of is negative, both these roots must be positive.