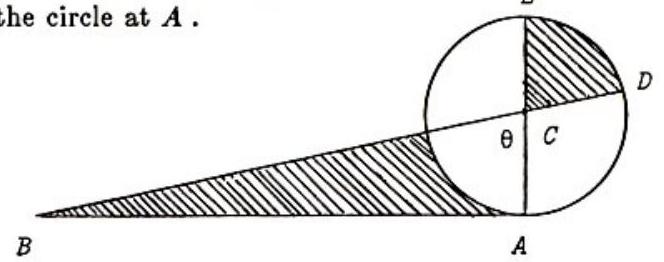
Problem:
In the configuration below, θ is measured in radians, C is the center of the circle, BCD and ACE are line segments, and AB is tangent to the circle at A.
A necessary and sufficient condition for the equality of the two shaded areas, given 0<θ<π/2, is
Answer Choices:
A. tanθ=θ
B. tanθ=2θ
C. tanθ=4θ
D. tan2θ=θ
E. tan2θ=θ
Solution:
The area of the shaded sector is 2θ(AC)2. This must equal half the area of △ABC, which is 21(AC)(AB). Hence the shaded regions have equal area iff 2θ(AC)2=41(AC)(AB), which is equivalent to 2θ=ACAB=tanθ.