Problem:
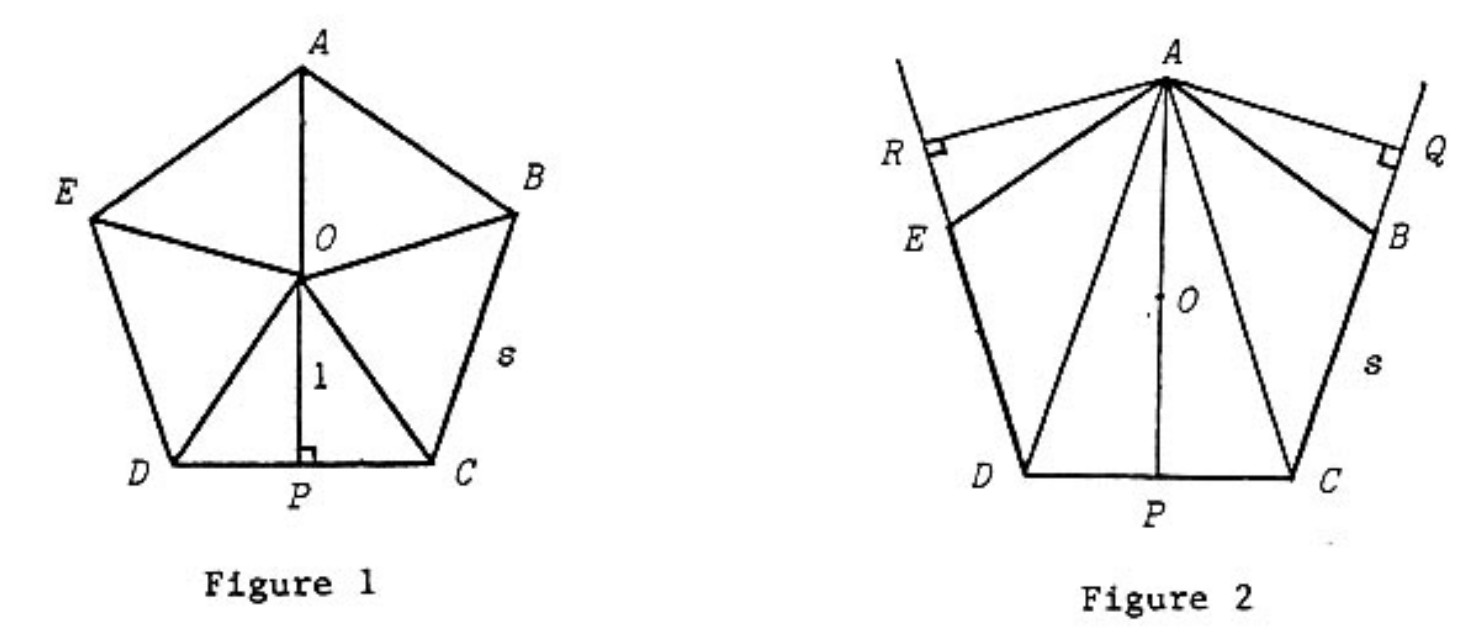
is a regular pentagon. dropped from onto extended and extended, respectively. Let be the center of the pentagon. If , then equals
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let denote the length of a side of the pentagon. We compute the area of in two ways. First (Figure ), it is the sum of the areas of the triangles and . Each of these has base and altitude . Thus the area of the pentagon is . On the other hand (Figure ), the area is the sum of the areas of the triangles and , which have base and altitudes and , respectively. Thus the total area is . Hence and .