Problem:
Two of the altitudes of the scalene triangle have length and . If the length of the third altitude is also an integer, what is the biggest it can be?
Answer Choices:
A.
B.
C.
D.
E. none of these
Solution:
Assume the altitude with length falls on side , the altitude with length falls on , and the unknown altitude with length falls on . Let be the area of . Then
By the triangle inequality, and . In other words,
These are equivalent to
Hence . If is an integer, it cannot exceed .
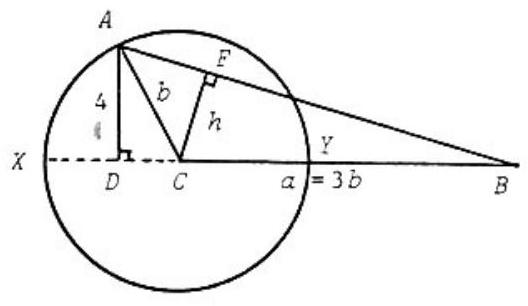
If the altitudes of a triangle are in a given ratio, the corresponding sides are in the inverse ratio. In particular, using the same notation as above, we have from . Thus, thinking of side as fixed, can be any point on the circle with center and radius as shown in the figure (except points and , which don't result in a triangle). Since , . Furthermore, would equal when and would equal when ). Thus
The largest integer value for is .
This solution also suggests how to construct a triangle with altitudes and . From (*), . Thus is an intersection point of the circle shown and the circle of radius centered at . There is only one hitch: this construction requires that you know to begin with. Do you see how to get around this problem?