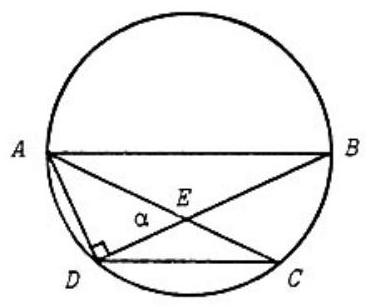
Problem:
In the adjoining figure, AB is a diameter of the circle, CD is a chord parallel to AB, and AC intersects BD at E, with ∠AED=α. The ratio of the area of △CDE to that of △ABE is
Answer Choices:
A. cosα
B. sinα
C. cos2α
D. sin2α
E. 1−sinα
Solution:
Because AB∥DC, arc AD=arcCB and CDE and ABE are similar isosceles triangles. Thus
Area ABE Area CDE=(AEDE)2
Draw in AD. Since AB is a diameter, ∠ADB=90∘. Thus, considering right triangle ADE,DE=AEcosα, and
(AEDE)2=cos2α