Problem:
There are two natural ways to inscribe a square in a given isosceles right triangle. If it is done as in Figure below, then one finds that the area of the square is . What is the area (in ) of the square inscribed in the same as shown in Figure below?
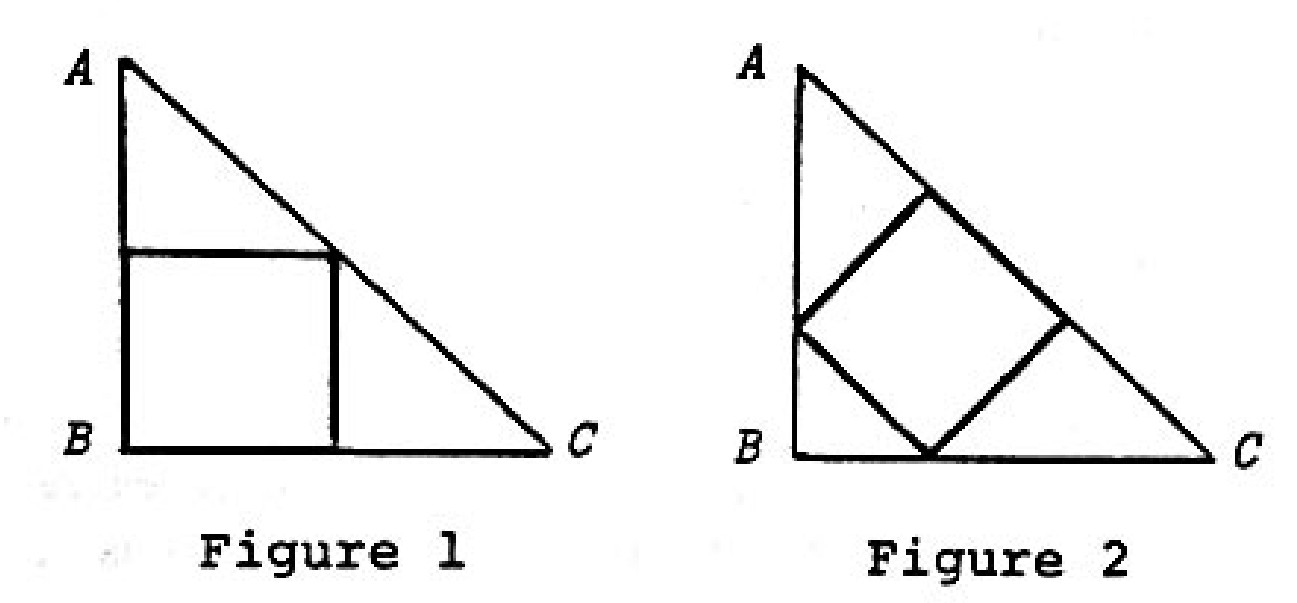
Answer Choices:
A.
B.
C.
D.
E.
Solution:
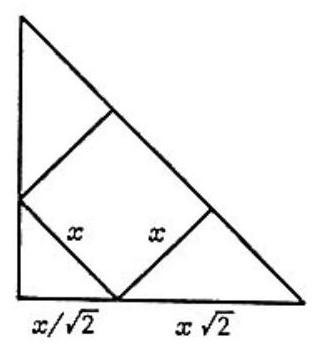
First observe that the legs of the triangle are twice as long as the sides of the first inscribed square, so the legs have length . Now, let be the side of the second inscribed square, as in the figure to the right. Note that all triangles in the figure are similar isosceles right triangles. Thus
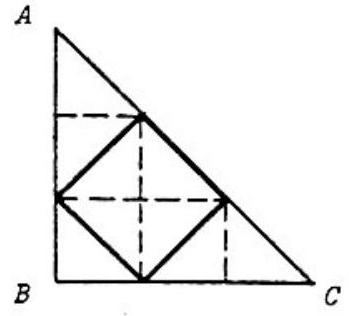
The area of is . Subdivide the area of as shown on the right, and observe that of the congruent isosceles right triangles into which is partitioned are inside the square inscribed the second way. It follows that the area of that square is .