Problem:
The amount is split into two nonnegative real numbers uniformly at random, for instance, into and , or into and . Then each number is rounded to its nearest integer, for instance, and in the first case above, and in the second. What is the probability that the two integers sum to
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the first number, the second. We solve the problem graphically. By running the number line for backwards, we can put directly over as follows:
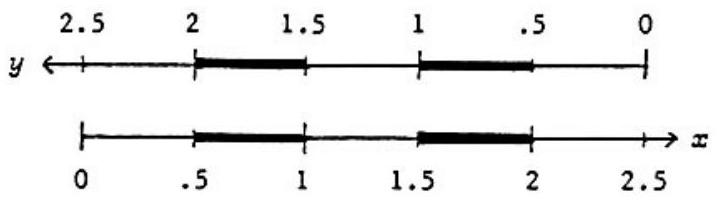
We have marked in bold the segments of their number lines where and are rounded up. We see that either they are both rounded up (in which case the resulting integers add to ) or they are both rounded down (in which case the resulting integers don't add to ). Since the bold segments for have combined length out of a total length of , and the probability distribution for is uniform, the answer is .
Note. We haven't worried whether and are rounded up or down. Why doesn't it make any difference?