Problem:
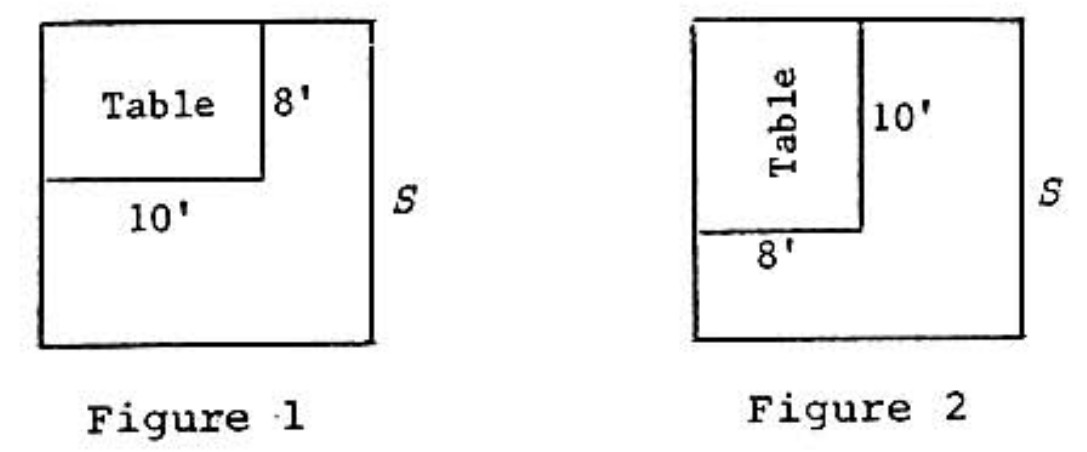
An table sits in the corner of a square room, as in Figure below. The owners desire to move the table to the position shown in Figure . The side of the room is feet. What is the smallest integer value of for which the table can be moved as desired without tilting it or taking it apart?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Consider either diagonal of the table. It has length . At some point in turning the table, this diagonal must be perpendicular to a pair of opposite walls of the room. Thus . This necessary condition is also sufficient: imagine a circle of diameter within the room, translate the table so that it is inscribed in this circle, rotate the table , and then translate it into the desired corner. The smallest integer satisfying is .