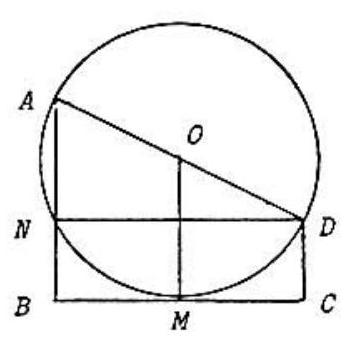
Problem:
In the figure, , and is tangent to the circle with center and diameter . In which one of the following cases is the area of an integer?
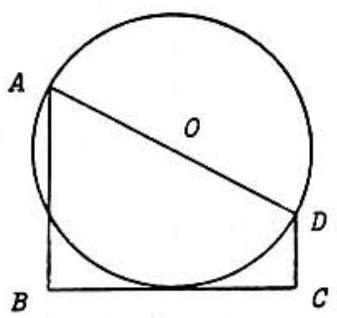
Answer Choices:
A. ,
B. ,
C. ,
D. ,
E. ,
Solution:
is a trapezoid, hence its area is . With an eye on the answers, we seek to express in terms of and . Let be the point where is tangent to the circle, and let be the point where intersects the circle. is right because is a diameter. Thus is a rectangle and . is right because is a tangent. Thus is parallel to and is the midpoint of . A standard theorem about tangents and secants to circles now states that , so that . Hence the area of is . This is an integer iff is a perfect square, since and are integers in all the choices given. Thus the answer is .