Problem:
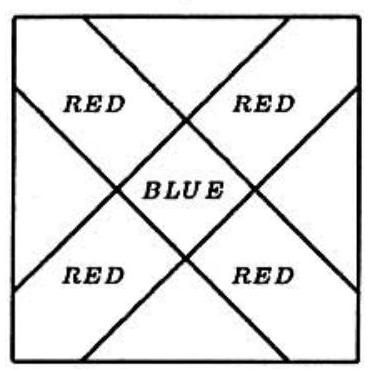
A square flag has a red cross of uniform width with a blue square in the center on a white background as shown. (The cross is symmetric with respect to each of the diagonals of the square.) If the entire cross (both the red arms and the blue center) takes up of the area of the flag, what percent of the area of the flag is blue?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
.jpg)
Let the total area be and let each red segment on the border of the flag be of length . Then the four white triangles can be placed together to form a white square of area and side . Thus and the blue area is , which is of the total area.
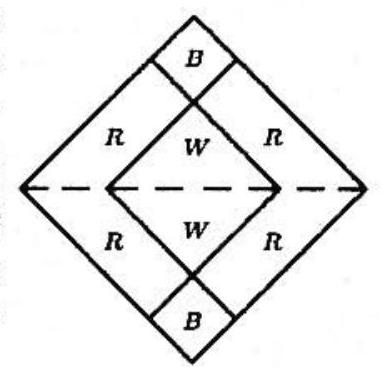
First note that the flag can be cut into four congruent isosceles right triangles by the two diagonals of the flag and that the percent of red, white, and blue areas in each of these triangles is the same as that in the flag. Then form a square by attaching two of these triangles along their hypotenuses as shown. For simplicity assume that this "half-flag" is a square. The interior white square consists of of the area, so it must be . Thus the two blue squares measure , so they constitute of the area.