Problem:
A regular octahedron is formed by joining the centers of adjoining faces of a cube. The ratio of the volume of the octahedron to the volume of the cube is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
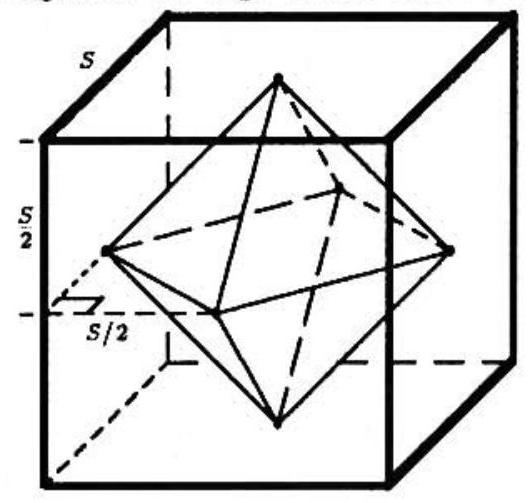
Without loss of generality, let the length of an edge of the cube be . Then the volume of the cube is and each edge of the octahedron is . Bisect the octahedron into two pyramids with square bases.
Each of the pyramids has altitude and a base of area , so the volume of each pyramid is . The volume of the octahedron is thus , so the required ratio is .
The bases of the two pyramids that make up the octahedron each have area equal to half the area of a face of the cube. The height of each pyramid is half the height of the cube. Thus
Note. More generally, if we form an octahedron by joining the centers of the six faces of any rectangular solid, then the volume of the octahedron is exactly one sixth of the volume of the rectangular solid.
Query. Is the hypothesis of perpendicularity in the preceding generalization a necessary one? Can you state and prove a further generalization?